2-Dimensionale meetkunde: kegelsneden: Parabolen
 Het begrip parabool
Het begrip parabool
De parabool is over het algemeen bekend als de verzameling oplossingen van de vergelijking #y=x^2# of, algemener, #y=a\cdot x^2+b\cdot x + c#, waarbij #a#, #b# en #c# reële getallen zijn. Maar als je deze grafiek draait in het vlak, dan is de figuur nog steeds een parabool, maar heeft het niet meer die vergelijking. Daarom noemen we de oplossingen van bovenstaande vergelijking liever een verticale parabool. Hieronder staat een meetkundige beschrijving van de parabool, die niet van draaiingen of spiegelingen afhangt.
Parabool
Een parabool is een verzameling punten in het vlak die gelijke afstand hebben tot een vast punt #F# en een vaste lijn #l#. Het punt #F# noemen we de focus en de lijn #l# de directrix van de parabool.
Als we #F = \rv{0,\frac{1}{4}}# en #l# de horizontale lijn met vergelijking #y=-\frac{1}{4}#, dan heeft een punt #\rv{x,y}# afstand #\sqrt{x^2+\left(y-\frac{1}{4}\right)^2}# tot #F# en #\left|y+\frac{1}{4}\right|# tot #l#, zodat de parabool met focus #F# en directrix #l# bestaat uit de verzameling punten #\rv{x,y}# met
\[\sqrt{x^2+\left(y-\frac{1}{4}\right)^2}=\left|y+\frac{1}{4}\right|\tiny.\]
Door links en rechts te kwadrateren vinden we
\[{x^2+\left(y-\frac{1}{4}\right)^2}=\left(y+\frac{1}{4}\right)^2\tiny.\]
Vereenvoudiging van deze vergelijking leidt tot #y=x^2#. Dit laat zien dat het standaardvoorbeeld van een parabool inderdaad een focus (namelijk #F#) en een directrix (namelijk #l#) heeft.
De vergelijking van een parabool
Elke parabool is de verzameling oplossingen van een kwadratische vergelijking die de vorm \[(a\cdot x+b\cdot y)^2 + p\cdot x+q\cdot y+r=0\] heeft, waarbij #a#, #b#, #p#, #q#, #r# reële getallen zijn, met ten minste één van #a#, #b# ongelijk aan #0#.
Om dit in te zien, schrijven we #F=\rv{u,v}# en #bx-ay+c=0# voor de vergelijking van #l#. Omdat de oplossingsverzameling van de vergelijking een lijn is, moet ten minste één van #a#, #b# ongelijk aan #0# zijn. Laat #P=\rv{x,y}# een willekeurig punt van het vlak zijn. Dan behoort #P# dan en slechts dan tot de parabool met focus #F# en directrix #l# als #|PF| # gelijk is aan de afstand van #P# tot #l#. De afstand van #P# tot #l# is volgens de theorie Afstand van punt tot lijn gegeven door de formule #\frac{|bx-ay+c| }{\sqrt{a^2+b^2}}#. Merk op dat #a^2+b^2# ongelijk is aan #0#.
Omdat beide afstanden niet-negatieve getallen zijn, zijn de twee afstanden dan en slechts dan gelijk als hun kwadraten gelijk zijn:\[\left(x-u\right)^2+\left(y-v\right)^2 = \frac{(bx-ay+c)^2 }{a^2+b^2}\tiny.\] Door de term #(bx-ay+c)^2# uit te schrijven als #(ax+by)^2+2c\cdot (ax+by)+c^2# en vervolgens alle termen te vermenigvuldigen met #a^2+b^2# kunnen we deze vergelijking herschrijven als\[(ax+by)^2 +p\cdot x+q\cdot y+r=0\]waarbij \[\begin{array}{rcl}p&=&-2b\cdot c-2(a^2+b^2)\cdot u\\ q&=&2a\cdot c-2(a^2+b^2)\cdot v\\ r&=&(a^2+b^2)\cdot (u^2+v^2)-c^2 \end{array}\]
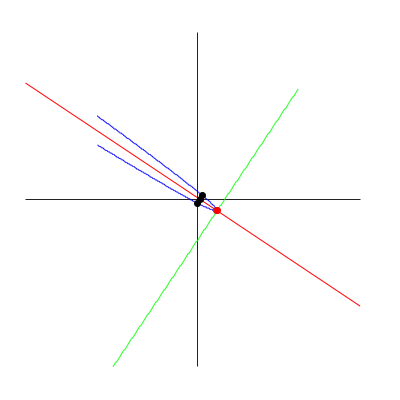
Vanwege de theorie is de richtingsvector van de symmetrie-as van de parabool gelijk aan #\rv{3,-2}#.
We zoeken een punt op de parabool. Daartoe nemen we #x=0# en lossen we de vergelijking met onbekende #y# op die uit #\left(2\cdot x+3\cdot y\right)^2-x-5\cdot y-6=0# ontstaat door #x=0# te stellen. Dit levert #y={{5-\sqrt{241}}\over{18}}#, zodat #A:=\rv{0,{{5-\sqrt{241}}\over{18}}}# een punt op de parabool is.
We zoeken vervolgens de coördinaten van het punt #B# op de lijn door #A# die evenwijdig aan de directrix is. Laatstgenoemde lijn heeft parametervoorstelling #A+\lambda\cdot\rv{2,3}=\rv{2\lambda,{{5-\sqrt{241}}\over{18}} +3\lambda}# omdat #\rv{2,3}# vanwege de theorie een richtingsvector van de directrix is. We vinden de waarde van #\lambda# die het punt #B# oplevert door #x=2\lambda# en #y={{5-\sqrt{241}}\over{18}} +3\lambda# in de vergelijking voor de parabool in te vullen. De vergelijking met onbekende #\lambda# die zo ontstaat luidt:\[ 169\cdot \lambda^2-{{13\cdot \sqrt{241}\cdot \lambda}\over{3}}+{{14 \cdot \lambda}\over{3}}=0\tiny.\]De oplossing #\lambda=0# leidt tot het bekende punt #A#, maar de andere oplossing, #\lambda={{13\cdot \sqrt{241}-14}\over{507}}#, geeft \[\begin{array}{rcl}B &=& \rv{2\cdot {{13\cdot \sqrt{241}-14}\over{507}},{{5-\sqrt{241}}\over{18}} +3\cdot {{13\cdot \sqrt{241}-14}\over{507}}}\\ &=& \rv{{{26\cdot \sqrt{241}-28}\over{507}},{{65\cdot \sqrt{241}+593}\over{3042}}}\end{array}\]
Het middelpunt #C=\frac{1}{2}(A+B)=\rv{{{13\cdot \sqrt{241}-14}\over{507}},{{719-52\cdot \sqrt{241}}\over{3042}}}# van het lijnstuk #AB# ligt op de symmetrieas van de parabool. Omdat zijn richtingsvector loodrecht staat op de richtingsvector van de referentielijn, heeft de symmetrieas parametervoorstelling\[ \rv{{{13\cdot \sqrt{241}-14}\over{507}},{{719-52\cdot \sqrt{241}}\over{3042}}}+\mu\cdot\rv{3,-2}\tiny.\]Deze symmetrieas snijdt de parabool in het punt #D# waarvoor de #x#-coördinaat en #y#-coördinaat voldoen aan de vergelijking van de parabool. Dit geeft de vergelijking
\[7\cdot \mu+{{7\cdot \sqrt{241}}\over{117}}-{{40925}\over{6084}}=0\tiny.\]De oplossing van deze vergelijking is #\mu={{40925-364\cdot \sqrt{241}}\over{42588}}#. Dat wil zeggen dat het snijpunt van de symmetrieas en de parabool gelijk is aan \[\begin{array}{rcl}D &=& \rv{{{13\cdot \sqrt{241}-14}\over{507}},{{719-52\cdot \sqrt{241}}\over{3042}}}+{{40925-364\cdot \sqrt{241}}\over{42588}}\cdot\rv{3,-2} \\ &=&\rv{{{13511}\over{4732}},-{{1994}\over{1183}}}\end{array}\]
Ook de focus #F# ligt op de symmetrieas. Het is dus van de vorm #\rv{{{13\cdot \sqrt{241}-14}\over{507}},{{719-52\cdot \sqrt{241}}\over{3042}}}+\nu\cdot\rv{3,-2}# voor een nog te vinden waarde #\nu#. De loodrecht projectie #P# van #F# op de referentielijn #l# ligt ook op de symmetrieas en de afstand van #D# tot #F# moet gelijk zijn aan de afstand van #D# tot #P#, omdat #D# op de parabool ligt. Dit betekent dat #P = \rv{{{13\cdot \sqrt{241}-14}\over{507}},{{719-52\cdot \sqrt{241}}\over{3042}}}+({{40925-364\cdot \sqrt{241}}\over{42588}}+\nu)\cdot\rv{3,-2}#.
Om de focus #F# te bepalen gebruiken we het feit dat #F# ligt op de symmetrieas en dat de afstand #|AF|# gelijk is aan de afstand van #A# tot de referentielijn. Omdat #ACPQ#, waarbij #Q# de loodrechte projectie van #A# op de referentielijn is, een rechthoek is, is deze laatste afstand is gelijk aan #|CP|#. Gelijkstellen van #|AF|^2# en #|CP|^2# levert de volgende vergelijking.\[ {{1028196\cdot \nu^2-364\cdot \sqrt{241}+40925}\over{79092}} = {{453434436\cdot \nu^2+\left(15502032\cdot \sqrt{241}-1742913900 \right)\cdot \nu-29793400\cdot \sqrt{241}+1706787161}\over{34879572 }}\tiny.\]De oplossing #\nu={{7408219\cdot \sqrt{241}-422184809}\over{3875508\cdot \sqrt{241}- 435728475}}# levert dat #F = \rv{{{257}\over{91}},-{{303}\over{182}}}# en #P=\rv{{{6829}\over{2366}},-{{4037}\over{2366}}}#. De referentielijn gaat door #P# en heeft richtingsvector #\rv{2,3}#, dus heeft vergelijking #3\cdot x-2\cdot y-{{169}\over{14}}=0#.
Om na te gaan dat we goede focus en referentielijn hebben, stellen we tenslotte nog de vergelijking op die uitdrukt dat voor het punt #\rv{x,y}# het kwadraat van de afstand tot #F# gelijk is aan de afstand tot #l#. Hierbij gebruiken we de formule voor de afstand van een punt tot een lijn.
\[\left(x-{{257}\over{91}}\right)^2+\left(y+{{303}\over{182}}\right)^2= \frac{(3x-2y-{{169}\over{14}})^2}{3^2+(-2)^2}\]Herschrijven door noemers weg te werken en gelijksoortige termen samen te voegen geeft de vergelijking\[4\cdot x^2+12\cdot y\cdot x-x+9\cdot y^2-5\cdot y-6=0\]waarvan eenvoudig na te gaan is dat ze overeenkomt met #\left(2\cdot x+3\cdot y\right)^2-x-5\cdot y-6=0#.

omptest.org als je een OMPT examen moet maken.



