Multivariate functies: Stationaire punten
Minimum, maximum en zadelpunt
De begrippen lokaal minimum en lokaal maximum kennen we al voor functies van één variabele. De functie \(f(x)\) heeft een lokaal minimum in \(x=a\) als de grafiek in de buurt van \(x=a\) boven \(f(a)\) ligt, preciezer gezegd, als er een open interval \(\ivoo{c}{d}\) om \(a\) is (dat wil zeggen: er getallen #c\lt a# en #d\gt a# zijn) zodanig dat \(f(x)\ge f(a)\) voor alle \(x\) uit \(\ivoo{c}{d}\). Voor de definitie in het geval van een functie van twee variabelen, vervangen we het open interval door een open cirkelschijf.
Lokale extremen
Laat #\epsilon# een positief getal zijn. De open cirkelschijf om een punt #p# van #{\mathbb R}^2# met straal #\epsilon# is de deelverzameling #S_{p,\epsilon}# van #{\mathbb R}^2# die bestaat uit alle punten #q\in {\mathbb R}^2# met afstand minder dan #\epsilon# tot #p#. In formulevorm:\[S_{p,\epsilon}=\left\{q\in{\mathbb R}^2\mid \sqrt{(p_1-q_1)^2 + (p_2-q_2)^2}\lt \epsilon\right\}\tiny.\]
Laat #f# een bivariate functie met domein #D# zijn en laat #p# een punt van #D# zijn.
- Het punt #p# heet een lokaal minimum van #f# als er een open cirkelschijf #S# om #p# ligt (dus een verzameling van de vorm #S=S_{p,\epsilon}# voor een geschikte waarde van #\epsilon#), zodat #f(q)\ge f(p)# voor alle #q\in D\cap S#.
- Het punt heet een lokaal maximum van #f# als er een open cirkelschijf #S# om #p# ligt, zodat #f(q)\le f(p)# voor alle #q\in D\cap S#.
- Het punt #p# heet een zadelpunt van #f# als het een stationair punt is, maar in elke open cirkelschijf om #p# punten \(q\) en \(r\) te vinden zijn zodanig dat \(f(q)\gt f(p)\) én \(f(r)\lt f(p)\).
Hieronder zie je de grafiek van de functie \[f(x,y)=\tfrac{1}{2}\!\left((1-(x-\tfrac{1}{2})^2-(y-\tfrac{1}{2})^2\right)\]
Deze functie heeft als partiële afgeleiden: \[f_x(x,y)=\tfrac{1}{2}-x\qquad\text{en}\qquad f_y(x,y)=\tfrac{1}{2}-y\] In het punt \(\rv{\tfrac{1}{2},\tfrac{1}{2}}\) zijn beide afgeleiden nul. Dit punt is dus een stationair punt. De functie heeft daar een maximale waarde.
Het begrip zadelpunt is vergelijkbaar met een stationair punt dat een buigpunt is bij een functie van één variabele.
Hier is de generalisatie van stelling Lokale extrema zijn stationaire punten voor één variabele.
Als #f# een differentieerbare bivariate functie is op een domein #D#, en #p# is een lokaal minimum of lokaal maximum van #f#, dan is #p# een stationair punt van #f#.
Het bewijs is eenvoudig: Schrijf #p=\rv{a,b}#. Dan is #a# een minimum of maximum van de differentieerbare functie #f(a,y)# in de variabele #y#. De stelling Lokale extrema zijn stationaire punten voor het geval van één variabele geeft dat \[\left.\frac{\partial f(x,y)}{\partial y}\right|_{\rv{a,b}}=\left.\frac{\dd f(a,y)}{\dd y}\right|_{b}=0\tiny.\]Net zo volgt \[\left.\frac{\partial f(x,y)}{\partial x}\right|_{\rv{a,b}}=\left.\frac{\dd f(x,b)}{\dd x}\right|_{a}=0\tiny.\]Dit betekent dat #p=\rv{a,b}# een stationair punt van #f# is.
Zadelpunten zijn per definitie ook stationaire punten die geen lokaal minimum en geen lokaal maximum zijn. De definitie van zadelpunt is zelfs zo gekozen dat een stationair punt van #f# altijd een minimum, maximum of een zadelpunt is.
Net als bij functies van één variabele is voor differentieerbare functies van twee variabelen de eis dat een punt een stationair punt is noodzakelijk maar niet voldoende om een punt een lokaal minimum of lokaal maximum te doen zijn. We geven een tegenvoorbeeld.
Hieronder zie je de grafiek van de functie \[f(x,y)=\tfrac{1}{2}\!\left((1-(x-\tfrac{1}{2})^2+(y-\tfrac{1}{2})^2\right)\]
Deze functie heeft als partiële afgeleiden: \[f_x(x,y)=\tfrac{1}{2}-x\phantom{quad}\text{en}\phantom{quad} f_y(x,y)=y-\tfrac{1}{2}\] In het punt \(\tfrac{1}{2},\tfrac{1}{2}\) zijn beide afgeleiden weer nul. Maar de coördinatenlijn is in de richting van de \(x\)-as een bergparabool, en de coördinatenlijn is in de richting van de \(y\)-as een dalparabool. Het punt \(\rv{\tfrac{1}{2},\tfrac{1}{2}}\) is dus een zadelpunt.
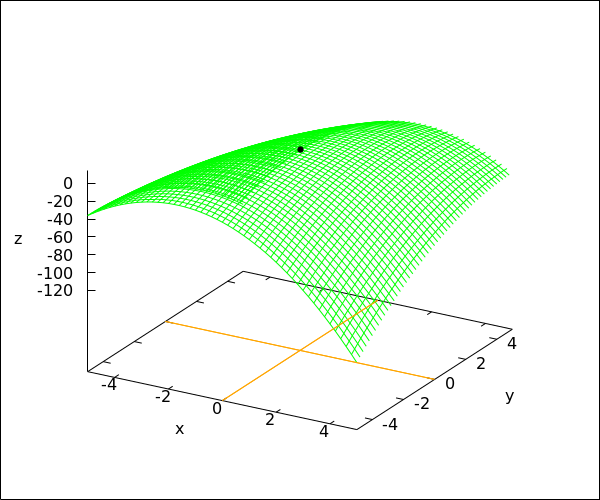
Omdat een lokaal maximum van een differentieerbare bivariate functie een stationair punt is, rekenen we eerst de stationaire punten uit. De partiële afgeleiden van #f# zijn \[f_x(x,y)=-4\cdot x-2\cdot y+36\phantom{quad}\text{en}\phantom{quad}f_y(x,y)=-2\cdot x-4\cdot y+42\tiny.\] De stationaire punten zijn dus de oplossingen van het stelsel vergelijkingen \[\lineqs{-4\cdot x-2\cdot y+36&=&0\cr -2\cdot x-4\cdot y+42&=&0\cr}\]
Dit stelsel heeft precies één oplossing: #{x = 5\land y = 8}#. We concluderen dat er precies één stationair punt is: #\rv{5, 8}#. Omdat gegeven is dat #f# een lokaal maximum heeft, moet dit punt wel het antwoord zijn: #\rv{5, 8}#.
De grafiek van de functie #f# is in de figuur hieronder getekend. Het lokale maximum #\rv{5,8,254}# is aangegeven met een kleine zwarte cirkelschijf.
omptest.org als je een OMPT examen moet maken.
