Fourier series: Coefficients of Fourier series
Calculation of Fourier coefficients
Calculate the Fourier series of the #2\pi#-periodic function #f# determined by \[f(x)=\left\{\begin{array}{l cl} 0& \phantom{x}\text{if} & -\pi \le x\lt 0 \\ 3 x & \phantom{x}\text{if}& 0\leq x\lt\pi\end{array}\right.\]
A plot of the function \( f \) over three periods is given in the figure below.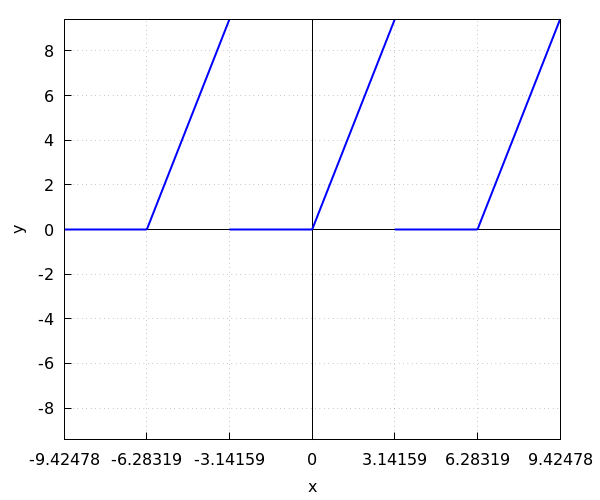
Enter simplified expressions for the coefficients \(a_0\), \(a_k\), and \(b_k\) \( (k=1,2,\dots)\), where the Fourier series is given by \[s(x)=\frac{a_0}{2}+\sum_{k=1}^{\infty}\left(a_k\cdot\cos\left(k\cdot x\right)+b_k\sin\left(k\cdot x\right)\right)\]
A plot of the function \( f \) over three periods is given in the figure below.
Enter simplified expressions for the coefficients \(a_0\), \(a_k\), and \(b_k\) \( (k=1,2,\dots)\), where the Fourier series is given by \[s(x)=\frac{a_0}{2}+\sum_{k=1}^{\infty}\left(a_k\cdot\cos\left(k\cdot x\right)+b_k\sin\left(k\cdot x\right)\right)\]
| \(a_0=\) |
| \(a_k=\) | for \(k=1,2,3,\dots\) |
| \(b_k=\) | for \(k=1,2,3,\dots\) |
Unlock full access
Teacher access
Request a demo account. We will help you get started with our digital learning environment.
Student access
Is your university not a partner?
Get access to our courses via Pass Your Math independent of your university. See pricing and more.
Or visit omptest.org if jou are taking an OMPT exam.
Or visit omptest.org if jou are taking an OMPT exam.
